9.sınıf Matematik Sayılar Konu Anlatımı
KONU:SAYILAR
Rakam Nedir?
Sayıları ifade etmeye yarayan sembollere rakam denir. Onluk sistemde kullanılan rakamlar: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 dur.
Sayı Nedir?
Bir çokluk belirtmek için, rakamların belirli kurallara göre bir araya getirilmesiyle oluşan ifadeye sayı denir.
Sayı Kümeleri
Sayıların belirli özelliklere göre bir araya gelerek oluşturduğu kümelerdir.
Doğal Sayılar Kümesi (N)
Kümelerin eleman sayısını belirten sayılara, yani N={0, 1, 2, 3, 4, ….., n, n+1, ….} şeklinde sonsuza kadar giden kümenin elemanlarına doğal sayı denir. En küçük doğal sayı 0 (sıfır) dır.
a, b, c birer rakam olmak üzere
ab iki basamaklı bir sayı ise ab= 10a + b
abc üç basamaklı bir sayı ise abc= 100a + 10b + c şeklinde yazılabilir.
Tam Sayılar Kümesi (Z)
Pozitif tam sayılar, negatif tam sayılar ve sıfırın oluşturduğu kümeye tamsayılar kümesi denir. Z= {…., -n, …., -3, -2, -1, 0, 1, 2, 3, …., n, ….} dir.
- Z+ = {1, 2, 3, …, n, ….,} pozitif tam sayılar kümesi.
- Z– = {…, -n, …., -3, -2, -1} negatif tam sayılar kümesi.
- Z= Z– Z+ ve Z+ U {0} = N dir.
- 0 (sıfır) pozitif ya da negatif değildir, işareti olmayan bir tam sayıdır.
2 ile bölünebilen tam sayılara çift tam sayılar denir. k Z için 2k ile gösterilir. Çift tam sayılar kümesi: Ç= {…, -6, -4, -2, 0, 2, 4, ….} dir.
2 ile bölünemeyen tam sayılara tek tam sayılar denir. k Z için 2k+1 veya 2k-1 ile gösterilir. Tek tam sayılar kümesi: T= {…, -5, -3, -1, 1, 3, 5, ….} dir.
Ç=Çift tam sayılar ve T=Tek tam sayılarda işlemler aşağıdaki gibi gerçekleşir.
| ÇÇ=Ç | TT=Ç | TÇ=T |
| Ç.Ç=Ç | T.T=T | T.Ç=Ç |
| Tn =T (n Z+) | Çn =Ç (n Z+) |
Rasyonel Sayılar Kümesi (Q)
a ve b birer tamsayı ve b 0 olmak üzere, şeklinde yazılabilen sayılara rasyonel sayılar denir. Rasyonel sayılar kümesi Q ile gösterilir.
Q={}
, -3, 0, 2, … sayıları birer rasyonel sayıdır.
- ifadesindeki b değeri 1 alınır ise olur. Bu durumda a Q olur ve buradan yola çıkarak her tam sayı aynı zamanda bir rasyonel sayıdır diyebiliriz. Bu durumda Z Q olur.
- ifadesinde a0 b=0 olursa ifade tanımsız olur.
- ifadesinde a=0, b=0 olduğunda “belirsiz” olur.
- Q=Q– {0} Q+
Devirli Ondalık Sayılar
Bir sayının ondalık yazımında virgülden sonraki kısmı belirli bir kurala göre tekrar ediyor ise bu sayılara devirli ondalık sayılar denir. Virgülden sonraki ilk devreden sayı grubunun (tekrar eden kısım) üstüne çizgi çizilerek gösterilir.
1/3=0,033333=
1/2=0,50000 =
Her devirli ondalık sayı bir rasyonel sayıdır. Rasyonel karşılığını hesaplamak için verilen formül kullanılabilir.
İrrasyonel Sayılar Kümesi (Q’)
Virgülden sonraki kısmı bilinmeyen veya a, b, Z ve b 0 olmak üzere, şeklinde yazılamayan sayılara irrasyonel (rasyonel olmayan) sayılar denir.
İrrasyonel sayılar kümesi Q’ ile gösterilir. Q’= {x : x ; a, b Z ve b 0}
, …., e, ,… sayıları birer irrasyonel sayıdır.
Gerçek (Reel) Sayılar Kümesi (R)
Sayı doğrusundaki bütün sayılarla bire bir eşlenebilen sayıların oluşturduğu kümeye reel sayılar kümesi denir ve R ile gösterilir.
- R=Q Q’
- N+ =Z+ N Z Q R ve Q’ R dir.
Gerçek Sayılar Kümesinde Toplama İşleminin Özellikleri
- Kapalılık özelliği: a, b R için a + b R dir. Herhangi iki gerçek sayının toplamı yine bir gerçek sayıdır.
- Değişme özelliği: a, b R için a + b = b + a dır.
- Birleşme özelliği: a, b R için a + (b + c) = (a + b) + c dir.
- Etkisiz eleman özelliği: a R için a + 0 = a olduğu için toplama işleminde 0 etkisiz elemandır.
- Ters eleman özelliği: a R için a + (-a) = (-a) + a = 0 olacak şekilde -a değeri vardır. a sayısının toplama işlemine göre tersine -a sayısı denir.
Gerçek Sayılar Kümesinde Çarpma İşleminin Özellikleri
- Kapalılık özelliği: a, b R için a.b R dır.İki gerçek sayının çarpımı yine gerçek sayıdır.
- Değişme özelliği: a, b R için a.b= b.a olur.
- Birleşme özelliği: a, b R için a. (b.c)= (a.b). c dir.
- Etkisiz eleman özelliği: a R için a . 1 = 1 . a = a olduğundan 1 çarpma işleminde etkisiz elemandır.
- Ters eleman özelliği: a R – {0} için a. = . a = 1 olacak şekilde R sayısı tanımlıdır. a R – {0} sayısının çarpma işlemine göre tersi dır.
- Yutan eleman özelliği: Gerçek sayılar kümesinde 0 çarpmada yutan elemandır.
- Dağılma özelliği: a, b, c R için a.(b+c) = a.b + a.c, (b+c).a = b.a + c.a
a. (b-c) = a.b – a.c, (b-c). a = b.a – c.a dır. çarpma işleminin toplama ve çıkarma işlemi üzerine dağılma özelliği vardır.
Bölünebilme Kuralları
Konu Özeti
Tam sayılarda bölme algoritmalarından yola çıkarak devamında bölünebilme kuralları ve bazı sayılarda bölünebilme koşulları ele alınmıştır. Aynı zamanda asal çarpan ve tam sayı bölenleri de incelenmiştir.Bölme işlemi çarpma işleminin tersi olan aritmetik işlemdir. Bir bütünün istenilen sayı kadar eş parçaya ayrılması temeline dayanır.
Tam Sayılarda Bölme Algoritması
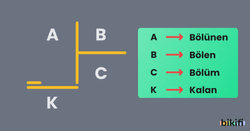
A, B, C, K tam sayılar ve olsun.
A: Bölünen
B: Bölen
C: Bölüm
K: Kalan
Yukarıdaki bölme işlemine göre,
- A=B.C + K
- K<B
- K=0 ise A sayısı B sayısına tam bölünür. Bu durum B|A şeklinde gösterilir.
Örnek: A sayısının B doğal sayısına bölümünden elde edilen bölüm 3 kalan 2 dir. Buna göre A sayısının alabileceği en küçük pozitif tam sayı değerini hesaplayalım.
Çözüm: A = 3B+2 dir. Kalan< bölen olduğundan 3<B olup B en az 4 olur. Buradan A’nın en küçük değeri, A=3B+2 3.4+2=14 olur.
Örnek: A ve x birer doğal sayı ve
olduğuna göre, A nın alabileceği en büyük değeri bulalım.
Çözüm: A=50.2.x + x2 şeklinde yazılabilir. A’nın en büyük olabilmesi için x in en büyük olması gerekir. x2 < 50 olduğuna göre, x en büyük 7 değerini alabilir. 7 değeri yerine yazılır ise A=50 .2 .7 + 72 = 749 olur.
A, B, x, m, n, c pozitif tamsayılar olmak üzere, A’nın x’e bölümünden kalan m, B’nin x’e bölümünden kalan n olsun.
- A.B nin x’e bölümünden kalan m.n dir.
- A B nin x’e bölümünden kalan m n dir.
- c.A’nın x’e bölümünden kalan c.m dir.
- Ac nin x’e bölümünden kalan mc dir.
Burada; m.n, mn, c.m ve mc sayıları x’ten küçük değilse bu değerler x’e tekrar bölünerek kalan belirlenir.
Asal Sayılar
Sadece kendisine ve 1 sayısına kalansız bölünebilen 1’den büyük tam sayılara asal sayı denir.
Aralarında Asal Sayılar
İki sayının 1 sayısından başka pozitif ortak böleni yoksa bu sayılara aralarında asal denir. Örneğin; 2 ile 3, 3 ile 4, 8 ile 15 sayıları aralarında asaldır.
Tam Sayılarda Bölünebilme Kuralları
Bu başlığın altında 2, 3, 4, 5, 6, 8, 9, 10 ve 11 ile bölünebilme kuralları incelenmiştir.
2 ile Bölünebilme
Çift sayılar 2 ile tam bölünür. Çift sayıların 2 ile bölümünden kalan sıfır, tek sayıların 2 ile bölümünden kalan ise 1’dir. Birler basamağında çift rakam {0, 2, 4, 6, 8} olan doğal sayılar 2 ile tam bölünür.
Bu kuralın nedenini inceleyelim. abc çok basamaklı bir doğal sayı ise 100a+10b+c şeklinde yazılabilir. 10 ve 10’un kuvvetleri 2’nin katı olduğundan 10b ve solunda bulunan terimler 2’ye tam bölünür. Bu yüzden sadece c’ye bakmak yeterli olur.
3 ile Bölünebilme
Bir doğal sayının rakamları toplamının 3 ile bölümünden kalan bu sayının 3 ile bölümünden kalana eşittir. 5672 sayısının 3 ile bölümünden kalan 5+6+7+2=20 elde edilir ve 20/3 işleminden kalan 2 olur. 5672 sayısının 3’e bölümünden kalan 2 olur.
Bu kuralın nedenini inceleyelim. abc çok basamaklı bir doğal sayı ise 100a+10b+c şeklinde yazılabilir. 10 ve 10’un kuvvetlerinin 3 ile bölümünden kalan 1 olduğu için sayıların yerine 1 yazılabilir. Bu durumda 100a+10b+c sayısında 10 ve kuvvetlerinin yerine 3 ile bölümünden kalanlar yazılır. 1a+1b+c şeklini alır ve rakamlar toplamı elde edilir.
4 ile Bölünebilme
Son iki (birler ve onlar) basamağı (iki basamaklı sayı gibi düşünülerek) 4’ün katı olan sayılar 4 ile tam bölünür, kalan için ise bu sayı 4 ile bölünerek bulunur.
1234 sayısının 4’e bölümünden kalanı hesaplayalım. 1234 sayısının son iki basamağı 34 olur ve 34 sayısının 4’e bölümünden kalan 1234 sayısının 4’e bölümünden kalana eşittir. 34=4.8+2 olduğundan 34 sayısının 4’e bölümünden kalan 2’dir.
5 ile Bölünebilme
Birler basamağı 0 veya 5 olan sayılar 5’e tam bölünür. Bir sayının 5’e bölümünden kalan, bu sayının birler basamağındaki rakamın 5’e bölümünden kalandır.
Bu kuralın nedenini inceleyelim. abc çok basamaklı bir doğal sayı ise 100a+10b+c şeklinde yazılabilir. 10 ve 10’un kuvvetleri 5’nin katı olduğundan 10b ve solunda bulunan terimler 5 ile tam bölünür. Bu yüzden sadece c’ye bakmak yeterli olur.
6 ile Bölünebilme
Hem 2 ile hem de 3 ile tam bölünebilen sayılar (3 ile tam bölünebilen çift sayılar) 6 ile tam bölünür.
8 ile Bölünebilme
Bir doğal sayının son üç basamağındaki rakamların oluşturduğu sayı, 8 in katı ise sayı 8 ile tam bölünür. Sayının 8 ile bölümünden kalan da aynı şekilde son üç basamağındaki sayının 8 ile bölümünden kalana eşittir.
6794120 sayısının 8 ile bölümünden kalan 0 dır. Sayı 8 e tam bölünür.
9 ile bölünebilme
Rakamlarının sayı değerlerinin toplamı 9 un katı olan sayılar 9 ile tam bölünür veya 9 ile bölümünden kalan da aynı şekilde rakamları toplamının 9 ile bölümünden kalana eşittir.
x ve y farklı iki sayı olmak üzere x5y4 dört basamaklı sayısı 9 ile tam bölündüğüne göre x + y değerini hesaplayalım.
x+5+y+4 değeri 9 a tam bölünüyor ise x + y 9 veya 18 olabilir fakat x ve y farklı olduğu için x+y=9 olur.
10 ile bölünebilme
Birler basamağı sıfır (0) olan sayılar 10 ile tam bölünür. Bir sayının birler basamağındaki sayı o sayının 10 ile bölümünden kalandır.
11 ile Bölünebilme
abcdef altı basamaklı bir sayı olsun. Sayının birler basamağından başlayarak sırasıyla rakamların önüne + ve – işaret yazılır ve rakamlar toplanır( -a +b -c +d -e +f). Oluşan bu toplam 11’in katı ise sayı 11’e tam bölünür. Bu toplam 11’e tam bölünmüyor ise kalan değer, sayının 11 ile bölümünden kalana eşittir.
Diğer Sayılara Bölünebilme
Aralarında asal iki sayıdan her birine bölünebilen bir sayı, bu sayıların çarpımına da bölünür.
Bir sayı aralarında asal olan a ve b sayısı gibi iki sayıya tam bölünüyor ise o sayı a.b değerine de tam bölünür.
2 ve 3’e tam bölünen bir sayı 6 ile tam bölünür. Bu yöntem ile birçok sayıya bölünebilme kuralı elde edilebilir.
- 12 ile bölünebilme kuralı; 3 ve 4’e tam bölünmeli
- 15 ile bölünebilme kuralı; 3 ve 5’e tam bölünmeli
- 18 ile bölünebilme kuralı; 2 ve 9’a tam bölünmeli
- 24 ile bölünebilme kuralı; 3 ve 8’e tam bölünmeli
- 30 ile bölünebilme kuralı; 3 ve 10’a tam bölünmeli
- 36 ile bölünebilme kuralı; 4 ve 9’a tam bölünmeli
şeklinde bulunur ve liste daha da uzatılabilir.
Tam Sayının Asal Çarpanları ve Tam Sayı Bölenleri
1’den büyük bütün sayılar asal çarpanlarının çarpımı şeklinde ayrılabilir. Bu, cebrin temel teoremlerinden biridir ve asal çarpanlara ayırma olarak adlandırılır.
120 sayısını asal çarpanlarına ayıralım.
| 120 | 2 |
| 60 | 2 |
| 30 | 2 |
| 15 | 3 |
| 5 | 5 |
| 1 |
2, 3, 5 sayıları 120’nin asal çarpanlarıdır.
Örnek: 800 sayısının asal sayı çarpanlarının toplamını bulalım.
Çözüm: 800 = 25 . 52 şeklinde yazılabilir. 800’ün 2 tane asal sayı böleni vardır. Bunlar 2 ve 5’dir. Asal sayı çarpanlarının toplamı 2+5=7 şeklinde hesaplanır.
Tam Bölen Kavramları
A sayısının asal çarpanlarına ayrılmış şekli, A = xa . yb . zc olsun. (x, y ve z asal sayılar. a, b ve c doğal sayılar.)
- A’nın (a+1).(b+1).(c+1) tane pozitif tam böleni vardır.
- A’nın pozitif bölenlerinin sayısı kadar negatif bölenleri olduğundan, 2.(a+1).(b+1).(c+1) tane tam böleni vardır.
- A’nın asal sayı bölenleri a, b, c olmak üzere 3 tanedir.
- A’nın tamsayı bölenleri toplamı 0’dır.
- A’nın asal sayı bölenleri hariç tamsayı bölenlerinin toplamı -(x+y+z) dir.
Örnek
600 sayısının pozitif bölenlerinin kaç tanesi,
- tektir?
- çiftir?
- 3’ün katıdır?
- 12’nin katıdır?
Çözüm
Öncelikle 600’ü asal çarpanlarına ayıralım.
| 600 | 2 |
| 300 | 2 |
| 150 | 2 |
| 75 | 3 |
| 25 | 5 |
| 5 | 5 |
| 1 |
- Tek olanı bulmak için, öncelikle çift olan asal çarpanları yok saymamız gerekiyor.
- Yani, . 31 . 52 asal çarpanları kalıyor.
- Tam bölen başlığındaki 1. kuraldan dolayı
- (1+1)*(2+1) = 2 * 3 = 6 tane pozitif böleni tek sayıdır.
- Çift olanı bulmak için,
- Çiftliğin sağlanması için bir tane 2 böleni kullanılmalıdır.
- Yani, 2 ( 22 . 31 . 52 ) olarak değerlendirilir.
- Parantez içine yine yukarıdaki kuralı uygularsak,
- (2+1)*(1+1)*(2+1) = 3 * 2 * 3 = 18 tane pozitif çift sayı böleni vardır.
- 3’ün katı olan bölenleri bulmak için,
- 3’e bölünebilmesi için bir tane 3 bölenini dışarıda tutmalıyız.
- Yani, 3 (23 . 52) olarak değerlendirilir.
- Parantez içine yukarıdaki kuralı uygularsak,
- (3+1) * (2+1) = 4 * 3 = 12
- 12’nin katı olan bölenleri bulmak için,
- 12’ye bölünebilmesi için 12’nin asal çarpanlarını (2 tane 2, 1 tane 3) dışarıda tutmalıyız.
- Yani, 12 ( 21 . 52) olarak değerlendirilir.
- Parantez içine yukarıdaki kuralı uygularsak,
- (1+1) * (2+1) = 2*3 = 6
Tam Sayı Bölenlerinin Toplamını Bulmak
A = xa . yb . zc olsun. A sayısının pozitif bölenleri toplamı şu şekilde hesaplanır:
Örnek: 150 sayısının 3’ün katı olan pozitif tam bölenleri toplamı kaçtır?
Çözüm:
- 150 sayısı 2 * 3 * 52 şeklinde yazılır.
- 3’ün katı olan pozitif tam bölenlerin toplamı istendiği için 3 (2 * 52) şeklinde ifade edilir.
- Toplam yukarıdaki formülden:
- (21+ 20) * (52+51+50) = 3 * 31 = 93
- Hesaplamanın dışında kalan 3 bütün toplama etki edeceği için elde edilen 93 sayısını dışarıda tutulan 3 sayısıyla çarpmalıyız.
- 93 * 3 = 279 bize 150 sayısının 3’ün katı olan pozitif tam bölenleri toplamını verecektir.
EBOB ve EKOK
Konu Özeti
İki veya daha fazla sayıyı birlikte bölebilen en büyük doğal sayıya bu sayıların en büyük ortak böleni (EBOB) denir. İki veya daha fazla sayının hepsinin birden katı olan en küçük doğal sayıya bu sayıların en küçük ortak katı (EKOK) denir. Bu değerler günlük hayattaki tekrar eden hesaplamalarda kullanılır.
En Büyük Ortak Bölen (EBOB)
İki veya daha fazla sayıyı birlikte bölebilen en büyük doğal sayıya bu sayıların en büyük ortak böleni denir ve EBOB şeklinde gösterilir.
18 ve 24 sayılarının bölenlerini incelersek
- 18 in tam sayı bölenleri: 18→{1, 2, 3, 6, 9, 18} şeklindedir.
- 24 ün tam sayı bölenleri: 24→{1, 2, 3, 4, 6, 8, 12, 24} şeklindedir.
- 18 ve 24 ün ortak pozitif tam sayı bölenleri: 1, 2, 3, 6 dır.
- 18 ve 24 ü ortak bölen en büyük tam sayı 6 olur.
- EBOB (18, 24)=(18, 24)EBOB =6 şeklinde yazılır.
18 ve 24 ün EBOB’u aşağıdaki gibi de bulunabilir.
| 1. Sayı | 2. Sayı | Bölen |
|---|---|---|
| 18 | 24 | |
| 9 | 12 | 2 |
| 9 | 6 | 2 |
| 9 | 3 | |
| 3 | 1 | 3 |
| 1 |
18 ve 24 ü ortak bölen sayıların çarpımı EBOB’u oluşturur. EBOB(18.24)=2.3=6 olur.
EBOB’un Hesaplanması
Sayıların EBOB değeri bulunurken sayılar asal çarpanlarına ayrılır ve ortak olan asal çarpanların üssü küçük olanları çarpılır.
Örnek: A= 24.3.57 , B=2.32.55 , C=3.53 sayılarının en büyük ortak böleni kaçtır?
Çözüm: EBOB, ortak asal çarpanların en küçük üstlülerinin çarpımı ile bulunur. Bu durumda EBOB(A, B,C)=3.53 tir.
EBOB Özellikleri
a, b, c, k pozitif tamsayı ve EBOB(a,b)=c olmak üzere
- EBOB(a, a)=a
- EBOB(k.b, b)=b
- EBOB(k.a, k.b)=k.c
- EBOB(, )=1
- a<b ise EBOB(a, b)≤a<b
- a ile b aralarında asal ise EBOB(a,b)=1’dir (ardışık tam sayılar ve ardışık tek sayılar aralarında asaldır).
En Küçük Ortak Kat (EKOK)
İki veya daha fazla sayının hepsinin birden katı olan en küçük doğal sayıya bu sayıların en küçük ortak katı denir ve EKOK şeklinde yazılır. EKOK(a,b) veya (a, b)EKOK şeklinde gösterilir.
18 ve 24 sayılarının EKOK’unu bulmak için sayıların katlarını hesaplayalım.
- 18’in pozitif tam sayı katları 18→{18, 36, 54, 72, 90, 108,126, 144, 162,…} şeklindedir.
- 24’ün pozitif tam sayı katları 24→{24, 48, 72, 96, 120, 144, 168,…} şeklindedir.
- 18 ve 24 sayılarının pozitif ortak katları 72, 144,…. olduğundan en küçük ortak kat 72 olur.
| 1.Sayı | 2.Sayı | Bölen |
|---|---|---|
| 18 | 24 | 2 |
| 9 | 12 | 2 |
| 9 | 6 | 2 |
| 9 | 3 | 3 |
| 3 | 1 | 3 |
| 1 | 1 |
18 ve 24’ün ortak katlarının en küçüğünü bulurken bölenlerin hepsini çarpmak gerekir. EKOK(18, 24)=23,32 =72 olur.
EKOK’un Hesaplaması
EKOK değeri bulunurken öncelikle sayıların asal çarpanları bulunur. Daha sonra ortak veya ortak olmayan asal çarpanlardan üssü büyük olanlarının çarpımı EKOK değerini verir.
Örnek: a, b, c asal sayılar olmak üzere. X=a5.b2.c , Y= a.b3.c6 , Z= b.c7olduğuna göre X, Y, Z sayılarının Ekok’unu hesaplayınız.
Çözüm: X, Y, Z sayıları asal çarpanlarına ayrılmıştır. Ekok hesabında asal çarpanların üssü büyük olanları çarpılır. X= .b2.c Y= a..c6 Z= b.EKOK(X, Y, Z)= a5.b3.c7 olur.
EKOK Özellikleri
a, b, c, k pozitif tamsayı ve EKOK(a,b)=c olmak üzere
- EKOK(a, a) = a
- EKOK(k.b, b) = k.b
- EKOK(k.a, k.b) = k.c
- a, b pozitif tam sayı olmak üzere EBOB(a, b) . EKOK(a, b) = a.b şeklinde ifade edilir.
- a ve b aralarında asal ise EBOB(a, b) = 1 ve EKOK(a, b) = a.b olur.
- a ve b pozitif tam sayı olmak üzere her a, b için, a<b ise EBOB(a, b)≤a<b≤EKOK(a,b)
- a, b, c, d pozitif tam sayılar olmak üzere
EKOK()=olur.
Periyodik Olarak Tekrar Eden Olay Uygulamaları
Bazı olaylar düzenli olarak belirli aralıklar ile tekrar eder. Bu olaylara periyodik olarak tekrar eden olaylar denir. Nöbet tutan bir hemşirenin nöbet döngüsü, spor yapan bir öğrencinin 3 günde bir spora gitmesi gibi olaylar periyodik olarak tekrar eden olaylara örnek verilebilir.
Örnek: Bugün cumartesi olduğuna göre 1587 gün sonra hangi gün olur?
Çözüm: Bir hafta 7 gün olduğuna göre her 7 günde bir yine cumartesi olacaktır. Bu durumda 1587 sayısını 7’ye bölersek geçen hafta sayısını buluruz ve kalan da cumartesiden sonra geçen gün sayısını verecektir. olur. Bu durumda 226 hafta + 5 gün sonrasını hesaplamamız gereklidir. Cumartesi den 5 gün sonrası perşembe olur.
Örnek:Bir öğrenci her gün yüzmeye gitmektedir. İlk çarşamba günü gittiğine göre 99 gün sonra hangi güne denk gelir.
Çözüm: Her 7 günde bir tekrar çarşamba olduğu için 99’un içinde kaç tane 7 varsa çıkardığımızda kalanı çarşambanın üstüne sayarak hangi gün olduğunu buluruz. 99=(14×7)+1 olur. Bu durumda çarşambadan 1 gün sonra olan perşembeyi buluruz yani öğrenci 99 gün sonra perşembe günü yüzmeye gider.
Örnek:Bir yemekhanede 2 günde bir pirinç pilavı, 5 günde bir baklava, 3 günde bir fırın tavuk yapılmaktadır. İlk pazar günü üçü birlikte yapıldığına göre 5. kez beraber yapıldığı gün hangi güne denk gelir.
Çözüm: 2, 3 ve 5’in en küçük ortak katı olan gün sonra tekrar aynı anda yapılırlar. EKOK(2,3,5)=30 olur. 5.kez birlikte yapılması için 4 defa daha birlikte yapılmaları gerekir. Bu durumda 30×4=120 gün sonra aynı gün yapılır. 120/7 den kalan 1 olur. Bu durumda pazartesi günü 5. kez aynı gün pirinç pilavı, fırın tavuk ve baklava yapılmış olur.
Gerçek Sayı Aralıkları
Konu Özeti
Gerçek sayı aralıkları matematikte sıklıkla kullanılan gösterimleri içermektedir. Gerçek sayılarda herhangi bir aralık belirtmek için 6 farklı yöntem vardır. Bunlar sırasıyla; kapalı aralık, açık aralık, yarı açık (yarı kapalı) aralık, üstten sınırsız aralık, alttan sınırsız aralık ve "R" aralığıdır.
Kapalı Aralık
a ve b birer gerçek sayı olmak üzere, a<b olsun. a ve b sayıları ile bu sayılar arasında kalan tüm gerçek sayılar a, b kapalı aralığını oluştururlar ve bu aralık [a, b] şeklinde gösterilir.
- [a, b]={x | a ≤ x ≤ b, x R} (Yukarıdaki resimde 1 numaralı grafik)
Açık Aralık
a, b kapalı aralığından a ve b sayıları çıkarılırsa a, b açık aralığı elde edilir ve a, b açık aralığı (a, b) şeklinde gösterilir.
- (a, b)= {x | a < x < b, x R} (Yukarıdaki resimde 2 numaralı grafik)
Yarı Açık (Yarı Kapalı) Aralık
a, b kapalı aralığından a ve b sayılarından sadece birisi çıkarılırsa yarı açık aralıklar elde edilir. Buna göre, a, b kapalı aralığından a sayısı çıkartılırsa (a,b], b sayısı çıkartılırsa [a,b) yarı açık aralığı oluşur.
- [a, b) = {x | a ≤ x < b, x R} (Yukarıdaki resimde 3 numaralı grafik)
- (a, b] = {x | a < x ≤ b, x R} (Yukarıdaki resimde 4 numaralı grafik)
Üstten Sınırsız Aralıklar
a R olmak üzere a dan büyük tüm gerçek sayıların kümesidir
- [a, ) = {x | a ≤ x, x R} (Yukarıdaki resimde 5 numaralı grafik)
- (a, ) = {x | a < x, x R} (Yukarıdaki resimde 6 numaralı grafik)
Alttan Sınırsız Aralıklar
a R olamk üzere a dan küçük tüm gerçek sayıların kümesidir.
- (, a] = {x | x ≤ a, x R}
- (, a) = {x | x < a, x R}
R aralığı
R nin kendisi de aralıktır. R=() = {x | R }
- R = (, ) = {x | < x < , x R} (Yukarıdaki resimde 7 numaralı grafik)
Denklemler
İçerisinde en az bir tane değişken bulunduran iki niceliğin birbirine eşitliğini ifade eden bağıntılara denklem denir.
Birinci Dereceden Bir Bilinmeyenli Denklemler
a, b R ve a 0 için ax + b = 0 şeklindeki ifadelere, x değişkenine (bilinmeyene) bağlı birinci dereceden bir bilinmeyenli denklem denir. a ve b denklemi katsayıları, x’e değişken denir. Denklemin derecesi değişkenin kuvvetine göre değişir.
Denklemi sağlayan x değerinin bulunmasına denklemi çözmek, denklemi sağlayan x R değerine denklemin kökü denir. Denklemin köklerinden oluşan kümeye, denklemin çözüm kümesi (Ç veya ÇK) denir.
- ax + b = 0 ifadesindeki terimlerde x değişkeninin üssü 1 olduğundan birinci dereceden bir denklem olur.
- ax + b = 0 denkleminde a 0 ise denklemin R de tek kökü vardır. Ç={-} olur.
- ax + b = 0 denkleminde çözüm kümesi R ise a=0 ve b=0 dır.
Birinci Dereceden İki Bilinmeyenli Denklemler
a, b, c R ve a 0, b 0 için ax+by+c=0 şeklindeki ifadelere x ve y değişkenlerine bağlı birinci dereceden iki bilinmeyenli denklem denir. Birinci dereceden iki bilinmeyenli bir denklemi gerçek sayılar kümesinde sağlayan sonsuz sayıda (x, y) ikilisi vardır ve bunlara denklemin çözüm kümesi denir. Çözüm kümesi analitik düzlemde bir doğru belirtir.
Örnek: 3x + 2y =6 denklem sistemini sağlayan (x, y) ikililerinin görüntü kümesini analitik düzlemde çizelim.
Çözüm: Düzlemdeki herhangi iki noktadan yalnızca tek doğru geçer. Denklemin çözüm kümesindeki ikililer aynı doğru üzerinde olur. Bu durumda doğrunun eksenleri kestiği noktayı bularak çizim yapabiliriz.
y eksenini kestiği noktada x=0 olur ve y=3 olur.
x eksenini kestiği noktada y=0 olur ve x=2 olur.
Bu durumda 3x + 2y =6 doğrusu (0, 3) ve (2, 0) noktalarında eksenleri keser ve aşağıdaki gibi çizilir.ax + by + c = 0 denklemi her x, y
R için sağlanıyorsa (Ç=R2 ) a=0, b=0, c=0 dır.
ax +by + c = 0 denkleminin çözüm kümesi boş küme ise a=0, b=0, c 0 dır.
Basit Eşitsizlikler
a, b R olmak üzere a<b, ab, b<a ya da ba şeklindeki ifadelere basit eşitsizlik denir.
x, y, a, b R olmak üzere basit eşitsizliklerin özellikleri aşağıdaki gibidir.
Bir eşitsizliğin her iki tarafına herhangi bir reel sayı eklenir ya da çıkarılır ise eşitsizlik değişmez.
Bir eşitsizliğin her iki tarafı pozitif bir sayı ile çarpılırsa eşitsizlik yön değiştirmez. Negatif bir sayı ile çarpılırsa eşitsizlik yön değiştirir.
Bir eşitsizliğin her iki tarafı pozitif bir sayı ile bölünürse eşitsizlik yön değiştirmez. Negatif bir sayı ile bölünür ise eşitsizlik yön değiştirir.
x<y ve y<z ise x<z dir. “<” işleminin geçişme özelliği vardır.
Aynı yönlü eşitsizlikler, taraf tarafa toplanabilir. Örneğin 2<9 ve 4<7 ise 2+4 < 9+7 ve 6<11 olur. Eşitsizliklerde taraf tarafa çıkarma, çarpma bölme işlemleri yapılamaz.
Pozitif sayılar arasındaki eşitsizliklerde her iki tarafın pozitif doğal sayı kuvveti alınırsa eşitsizlik yön değiştirmez.
Negatif sayılar arasındaki eşitsizliklerde her iki tarafın tek doğal sayı kuvveti alınırsa eşitsizlik yön değiştirmez. Sıfır dışındaki çift doğal sayı kuvveti alınırsa eşitsizlik yön değiştirir.
a, b R olmak üzere a<b, ab, b<a ya da ba şeklindeki ifadelere basit eşitsizlik denir.
x, y, a, b R olmak üzere basit eşitsizliklerin özellikleri aşağıdaki gibidir.
Bir eşitsizliğin her iki tarafına herhangi bir reel sayı eklenir ya da çıkarılır ise eşitsizlik değişmez.
Bir eşitsizliğin her iki tarafı pozitif bir sayı ile çarpılırsa eşitsizlik yön değiştirmez. Negatif bir sayı ile çarpılırsa eşitsizlik yön değiştirir.
Bir eşitsizliğin her iki tarafı pozitif bir sayı ile bölünürse eşitsizlik yön değiştirmez. Negatif bir sayı ile bölünür ise eşitsizlik yön değiştirir.
x<y ve y<z ise x<z dir. “<” işleminin geçişme özelliği vardır.
Aynı yönlü eşitsizlikler, taraf tarafa toplanabilir. Örneğin 2<9 ve 4<7 ise 2+4 < 9+7 ve 6<11 olur. Eşitsizliklerde taraf tarafa çıkarma, çarpma bölme işlemleri yapılamaz.
Pozitif sayılar arasındaki eşitsizliklerde her iki tarafın pozitif doğal sayı kuvveti alınırsa eşitsizlik yön değiştirmez.
Negatif sayılar arasındaki eşitsizliklerde her iki tarafın tek doğal sayı kuvveti alınırsa eşitsizlik yön değiştirmez. Sıfır dışındaki çift doğal sayı kuvveti alınırsa eşitsizlik yön değiştirir.
Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler
a, b R ve a 0 için ax+b≤0, ax+b<0, ax+b≥0, ax+b>0 şeklindeki ifadelere x değişkenine bağlı birinci dereceden bir bilinmeyenli eşitsizlik denir. Bu tür eşitsizliklerin çözüm kümesi, reel sayıların bir alt aralığıdır.
a, b R ve a 0 için ax+b≤0, ax+b<0, ax+b≥0, ax+b>0 şeklindeki ifadelere x değişkenine bağlı birinci dereceden bir bilinmeyenli eşitsizlik denir. Bu tür eşitsizliklerin çözüm kümesi, reel sayıların bir alt aralığıdır.
Birinci Dereceden İki Bilinmeyenli Eşitsizlikler
a, b R; a, b 0 olmak üzere ax+by+c0, ax+by+c0, ax+by+c0, ax+by+c0 şeklindeki ifadelere birinci dereceden iki bilinmeyenli eşitsizlik denir. (x, y) ikilisi eşitsizliği sağlar ve bu ikililerin kümesine eşitsizliğin çözüm kümesi denir. Çözüm kümesi analitik düzlemde boyalı olarak gösterilebilir.
ax+by+c=0 ifadesinde y, x e bağlı olarak yazılırsa by=-ax-c ve halini alır. Oluşan denklemde olarak yazılır ise denklem y=mx+n olur.
Oluşan yukarıdaki denklem ve çözüm kümesinin oluşturduğu analitik düzlem görüntüsünün özellikleri aşağıdaki gibi olur.
- y=mx+n denkleminin çözüm kümesi, doğru üzerindeki noktaları gösterir.
- y>mx+n eşitsizliğinin çözüm kümesi, y=mx+n doğrusunun üst bölgesidir.
- y<mx+n eşitsizliğinin çözüm kümesi, y=mx+n doğrusunun alt bölgesidir.
bulunması durumunda denklemin çözüm kümesinde doğru üzerindeki noktalarda yer alır ve düz çizgi olarak çizilir.
olması halinde denklemin çözüm kümesinde doğru üzerindeki noktalar yer almaz ve kesikli çizgi olarak çizilir.
a, b R; a, b 0 olmak üzere ax+by+c0, ax+by+c0, ax+by+c0, ax+by+c0 şeklindeki ifadelere birinci dereceden iki bilinmeyenli eşitsizlik denir. (x, y) ikilisi eşitsizliği sağlar ve bu ikililerin kümesine eşitsizliğin çözüm kümesi denir. Çözüm kümesi analitik düzlemde boyalı olarak gösterilebilir.
ax+by+c=0 ifadesinde y, x e bağlı olarak yazılırsa by=-ax-c ve halini alır. Oluşan denklemde olarak yazılır ise denklem y=mx+n olur.
Oluşan yukarıdaki denklem ve çözüm kümesinin oluşturduğu analitik düzlem görüntüsünün özellikleri aşağıdaki gibi olur.
- y=mx+n denkleminin çözüm kümesi, doğru üzerindeki noktaları gösterir.
- y>mx+n eşitsizliğinin çözüm kümesi, y=mx+n doğrusunun üst bölgesidir.
- y<mx+n eşitsizliğinin çözüm kümesi, y=mx+n doğrusunun alt bölgesidir.
bulunması durumunda denklemin çözüm kümesinde doğru üzerindeki noktalarda yer alır ve düz çizgi olarak çizilir.
olması halinde denklemin çözüm kümesinde doğru üzerindeki noktalar yer almaz ve kesikli çizgi olarak çizilir.
Mutlak Değer
Konu Özeti
Gerçek sayının sayı doğrusunda sıfır noktasına olan uzaklığına sayının mutlak değeri denir. x bir sayı ise mutlak değeri "|x|" ile gösterilir.
olarak tanımlanır.
Mutlak değer içindeki ifadenin gerçek sayı değeri 0 veya 0’dan büyükse mutlak değer dışına aynı çıkar. Fakat sayının değeri 0’dan küçük ise mutlak değer dışına çıkarken pozitif değer olması için negatif (-) işareti eklenerek çıkarılır.
- |5|=5
- |-5|=-(-5)=5
Mutlak Değerin Özellikleri
x ve y reel sayı ise
- |x|=|-x|
|x-y|=|y-x| - |xn|=|x|n
- k>0 için |k.x|=k.|x|
- |x.y|=|x|.|y|
- (Üçgen eşitsizliği)
Birinci Dereceden Mutlak Değerli Denklem ve Eşitsizlikler
Mutlak Değerli Denklemler
Mutlak değer bulunan denklemlere mutlak değerli denklemler denir. |x|=9 denkleminde x değişkeni 9 ve -9 olmak üzere iki farklı değer alır. Fakat |x| ifadesi sadece pozitif değer alır.
Özetlersek: x ve a reel sayı olmak üzere
- a0 için |x|=a veya x=-a olur.
- a<0 için |x|=a ise denklemin çözüm kümesi boş küme olur ve ÇK= olarak yazılır.
- |x|=|y| x=y veya x=-y olur.
- |x|=y x=y veya x=-y olur. x=y ve x=-y denklemleri ayrı ayrı çözülür ve bulunan kökler(x1, x2 ,…) yerine yazıldığında 0 durumunu sağlıyorsa çözüm kümesine dahil edilir.
Son yazdığımız özelliği aşağıdaki örnekte inceleyelim.
Örnek: |4x-7|=2x+5 denkleminin çözüm kümesini bulunuz.
olur. Bir değişken hem mutlak değer içinde hem de dışarıda kullanılmış ise, ilk denklemde yerine yazarak sağlaması yapılmalıdır. Mutlak değer negatif işaretli olamayacağı için kontrol edilmelidir.
6 ve 1/3 değeri denklemi sağladığı için ÇK={1/3, 6} olur.
Mutlak Değerli Eşitsizlikler
Mutlak değerli ifade eşitsizlik şeklinde ise mutlak değerli eşitsizlik denir. Mutlak değerli eşitsizlikler mutlak değerin tanımına göre çözülür.
I)a0 olmak üzere |x|
Örnek olarak |2x-4| 2 eşitsizliğinin çözüm kümesinin bulalım.
olur.
şeklinde yazılır. Ç.K = [1, 3] olur.
II)a 0 olmak üzere |x|
Örnek olarak |3x-12| 9 eşitsizliğinin çözüm kümesinin bulalım.
Ç.K= veya Ç.K= olur.
III) olmak üzere olur.
Örnek olarak eşitsizliğinin çözüm kümesinin bulalım.
Bu durumda olur.
IV) olur.
Konu Özeti
İçerisinde en az bir tane değişken bulunduran iki niceliğin birbirine eşitliğini ifade eden bağıntılara denklem denir. İki nicelik arasındaki büyük küçük olma durumunu belirten bağıntılara ise eşitsizlik denir. Bu iki kavramların özellikleri ve çözümleri ayrıntılı olarak incelenmiştir.
Birinci Dereceden İki Bilinmeyenli Denklem ve Eşitsizlik Sistemleri
Konu Özeti
Birinci dereceden iki bilinmeyenli denklem sistemlerinin ve birinci dereceden iki bilinmeyenli eşitsizlik sistemlerinin çözüm kümesini bulma yöntemlerini ve analitik düzlemde çözüm kümesini göstermeyi ele aldığımız bu konuda ayrıca açıklayıcı örnek sorular da bulunmaktadır.
Birinci dereceden iki bilinmeyenli denklem ve eşitsizlikleri önceki yazılarda tanımlamıştık. Bu yazıda ise denklem sistemlerini, çözüm yöntemlerini ve grafik çizimini ele alacağız.
Birinci Dereceden İki Bilinmeyenli Denklem Sistemleri
x ve y bilinmeyen, a ve b reel sayı, a1, a2, b1 ve b2 sıfırdan farklı olmak üzere
denklemlerinden oluşan sisteme birinci dereceden iki bilinmeyenli denklem sistemi denir. Bu denklemleri sağlayan x ve y gerçek sayılar ise (x, y) sıralı ikilisi olarak yazılır ve bu sıralı ikiliye denklemin çözüm kümesi denir. ax+by+c=0 birinci dereceden iki bilinmeyenli denklemlerinin grafikleri analitik düzlemde doğru belirtir. Bu denklemleri çözmek için yok etme, yerine koyma ve grafik çizimi gibi yöntemler kullanılır
Yok Etme Yöntemi
Denklem sisteminde aynı bilinmeyenlere sahip terimlerin katsayıları eşit ve ters işaretli olacak şekilde düzenlenir. Daha sonra taraf tarafa toplama yapılarak sadeleşmesi sağlanır.
Örnek olarak aşağıdaki denklem sisteminin çözüm kümesini bulalım.
denklemlerinde x bilinmeyenini yok etmek için ilk denklem 4 ikinci denklem -3 ile çarpılır.
Denklemler taraf tarafa toplanır ise 7y=-7 ⟹ y=-1 olur. y değeri herhangi bir denklemde yerine yazılır ise x değeri de bulunmuş olur. y=-1 ⟹ 3.x+4.(-1)=11 denkleminden x=5 bulunur.
Yerine Koyma Yöntemi
Denklem sistemindeki bilinmeyenlerden herhangi biri yalnız bırakılır ve diğer denklemde yerine yazılır. Bu yöntem ile çözüm kümesi elde edilebilir.
Örnek olarak
denklem sisteminin çözüm kümesini yerine koyma yöntemiyle bulalım.
x+5y=-5 denkleminde x yalnız bırakılır ise x=-5y-5 olur. İkinci denklemde x yerine -5y-5 yazılır ise 3(-5y-5)-2y=19 olur. y=-2 bulunur ve x değerini bulmak için herhangi bir denklemde y yerine -2 yazılır ise x=5 bulunur.
Grafik Yorumu
Birinci dereceden iki bilinmeyenli bir denklemin çözüm kümesinin oluşturduğu sıralı ikililer analitik düzlemde bir doğru belirtir. Denklem sisteminin oluşturduğu doğruların kesişim noktası veya noktaları bu denklem sisteminin çözüm kümesini oluşturur.
Örnek olarak
denklem sisteminin çözüm kümesini bulup grafiksel olarak yorumlayalım.
Dikkat edilir ise denklemler birbirinin katıdır. Bu durumda aslında iki denklem de aynı doğruyu oluşturur. Bu durumda doğrular çakışıktır ve çözüm kümesi sonsuz elemanlı olur.
Başka bir örnek olarak
denklem sisteminin çözüm kümesini bulup grafikte yorumlayalım.
İlk denklemde y bilinmeyenini yalnız bırakırsak y=8-2x olur ve ikinci denklemde y yerine bu değer yazılır ise x+3(8-2x)=9 elde edilir. 5x=15 ve x=3 olur. ÇK={(3, 2)} olur.
Denklemlerin eksenleri kestiği noktaları bulmak için sırasıyla x ve y yerine 0 yazılır.
İlk denklem de x=0 dersek y=8, y=0 dersek x=4 olur. Bu durumda ilk denklemin belirttiği d1 doğrusu (0, 8) ve (4, 0) noktalarından geçer (yeşil doğru).
İkinci denklem için de aynı yöntem uygulanır ise d2 doğrusu (9,0) ve (0, 3) noktalarında eksenleri keser (mavi doğru).
Şekilde de görüldüğü gibi kesişim noktası aynı zamanda çözüm kümesi olan A(3, 2) noktasıdır.ax+by+m=0 ve cx+dy+n=0 denklem sisteminin belirttiği doğrular ile ilgili aşağıdaki yorumlar yapılabilir.
- ise doğrular çakışıktır ve çözüm kümesinde sonsuz eleman vardır.
- ise doğrular paraleldir ve çözüm kümesi boş kümedir.
- ise doğrular tek noktada kesişir ve çözüm kümesi bir elemanlıdır.
Birinci Dereceden İki Bilinmeyenli Eşitsizlik Sistemleri
a, b, c birer gerçek sayı, a, b sıfırdan farklı olmak üzere
şeklindeki ifadelere birinci dereceden iki bilinmeyenli eşitsizlik denir. Birinci dereceden iki bilinmeyenli denklemlerde olduğu gibi bu eşitsizliğin çözüm kümesi de(x, y) şeklinde sıralı ikiliden oluşur. Eşitsizliği doğru yapan sonsuz sayıda sıralı ikili bulanacağı için çözüm kümesi analitik düzlemde boyalı bölgeler çizilerek gösterilir.
bulunan eşitsizliklerde doğru kesiksiz (düz) çizgi olarak çizilir. < veya > olması durumunda kesikli çizgi olarak çizilir. Eşitsizlik analitik düzlemde çizildiğinde düzlem iki bölgeye ayrılır. Ayrılan bu bölgelerden hangisinin çözüm kümesi olduğunu bulmak için bölgelerden herhangi bir nokta seçilir ve eşitsizlikte yazılır. Eşitsizliği sağlayan noktanın olduğu bölge taranır.
Aşağıdaki örnekte bir çözüm anlatılmıştır.
2x-5y<20 ve eşitsizlik sisteminin çözümünü analitik düzlemde gösteriniz.
2x-5y<20 için x ve y değerlerine sırasıyla 0 verilerek eksenleri kestiği noktalar bulunur. x=0 için y=-4 ve y=0 için x=10 olur. Sonuç olarak ilk eşitsizlik eksenleri (0,-4) ve (10,0) noktalarında keser. 2x-5y<20 ifadesinde (0,0) noktası yazılırsa 0<20 olur ve eşitsizliği sağladığı görülür. Bu durumda çözüm kümesi olarak doğrunun üst bölgesi alınır fakat eşitlik olmadığı için doğru çözüm kümesine dahil olmaz ve kesikli çizgi ile gösterilir.
için yine aynı yöntem uygulanır ise eşitsizlik (0,-5) ve (5,0) noktalarında eksenleri keser. ifadesinde (0,0) noktası yazılır ise olur ve nokta eşitsizliğin çözüm kümesine dahil değildir. Bu durumda doğrunun alt bölgesi çözüm kümesi olarak alınır ve doğru da çözüm kümesine dahil olduğu için düz çizgi olarak çizilir..
İki eşitsizliğin çözüm kümelerini temsil eden mavi ve kahverengi bölgelerin kesişimi yeşil bölgedir ve eşitsizlik sisteminin çözüm kümesidir.
Üslü İfadeler ve Denklemler Denklemler
Bir Gerçek Sayının Tam Sayı Kuvvetleri
olmak üzere an ifadesine üslü ifade adı verilir. an ifadesinde a sayısına taban, n sayısına ise üs veya kuvvet denir.
olarak hesaplanır.
Aşağıda örnek olarak bir üslü ifade verilmiştir.
Bir Gerçek Sayının Negatif Kuvveti
olmak üzere olur. olur.
Üslü Sayılarda Toplama ve Çıkarma İşlemi
Hem tabanı hem üssü aynı olan üslü sayılar ortak paranteze alınarak toplanabilir veya çıkarılabilir. olmak üzere olur.
Üslü Sayılarda Çarpma ve Bölme
Tabanları aynı olan üslü sayılar çarpılabilir. olmak üzere olur.
olmak üzere olur.
Üslü İfadelerin Bazı Özellikleri
- olur.
- belirsizdir.
- olmak üzere ve olur.
- olmak üzere olur.
- olmak üzere olur.
- olmak üzere
- Üslü sayılarda büyüklük, küçüklük kıyaslaması yaparken üsleri veya tabanları eşitleyerek hesaplamak gerekir.
Üslü Denklemler
Üslü sayı içeren denklemlere denir ve bazı özellikler sayesinde bu denklemler kolaylıkla çözülebilir. Bu özellikler aşağıdaki gibidir.
- olmak üzere ise olur. Tabanları eşit, iki üslü sayının üsleri de eşittir.
- olmak üzere
üsleri aynı olan iki üslü ifade eşit ise üs tek olduğunda tabanlar eşittir. Eğer üsleri aynı ve çift ise tabanlar mutlak değerce eşittir.
- eşitliği için
şeklinde üç farklı durum vardır.
- olmak koşuluyla
ilk koşul sağlanır.
Köklü Sayılar
Konu Özeti
a bir reel sayı ve n>2 olmak üzere x üzeri n = a eşitliğini sağlayan x sayısına a nın n. dereceden kökü denir ve x=n. dereceden kök a şeklinde okunur. Köklü ifadelerle ilgili özellikleri iyi kavramak için üslü ifadeleri bilmek oldukça önemlidir çünkü birçok kuralın dayanak noktası buradan gelmektedir.
a bir reel sayı ve n2 olmak üzere xn=a eşitliğini sağlayan x sayısına a nın n. dereceden kökü denir ve şeklinde gösterilir.
olur.
Her köklü sayıyı üslü sayı şeklinde yazabiliriz. şeklinde yazılabilir.
Köklü ifadeler,
- n=2 için, ; karekök a
- n=3 için, ; küpkök a
- n=4 için, ; dördüncü dereceden kök a
şeklinde okunur.
- ifadesinin bir reel sayı belirtmesi için; olmalıdır.
- ifadesi a nın bütün reel sayı değerleri için bir reel sayı belirtir.
Köklü İfadeyi Üslü İfade Olarak Yazma
Her köklü sayı üslü sayı olarak yazılabilir.
| Köklü İfade | Üslü İfade |
|---|---|
| a | |
| m tek sayı ise | a |
| m çift sayı ise | |a| |
Köklü İfadenin Üssünün Alınması
Köklü ifadelerin üssü şu şekilde alınabilir:
- =
Bir İfadeyi Kök İçine Alma veya Kök Dışına Çıkarma
b>0 olmak üzere,
- n tek sayı ise,
- n çift sayı ise,
Örnekler
ifadelerini kök içine alarak ve ifadelerini kök dışına çıkararak yazınız.
Kök Dışındaki Bir Çarpanın Kök İçine Yazılması
n. kuvvetten bir kökün dışında çarpım halinde bulunan bir ifade, n. kuvvetti alınarak kök içinde yazılabilir.
şeklinde ifade edilir. (n çift sayı ise olmalıdır.)
Kök Kuvvetinin Genişletilmesi veya Sadeleştirilmesi
Bir köklü ifadenin kuvveti ile kök içindeki ifadenin üssü aynı pozitif tam sayı ile tanım şartlarına uygun bir şekilde çarpılabilir( kök kuvvetini genişletme) veya bölünebilir (kök kuvvetini sadeleştirme).
r pozitif tam sayı olmak üzere,
Köklü İfadelerde Toplama – Çıkarma İşlemleri
İki köklü ifadenin toplanabilmesi (veya çıkarılabilmesi) için bu iki ifadenin kök kuvveti aynı ve köklerin içindeki ifadeler de birbirine eşit olmalıdır.
Örneğin;
- toplanamaz çünkü kök içindeki sayılar farklıdır.
- çıkarılamaz çünkü kök kuvvetleri farklıdır.
- dir.
Köklü İfadelerde Çarpma – Bölme İşlemleri
Kök kuvvetleri aynı olan köklü ifadeler çarpılabilir veya bölünebilir.
olur.
Örneğin;
Paydayı Kökten Kurtarma (Rasyonel Yapma)
Paydasında köklü terim bulunan bir kesrin paydasını kökten kurtarma işlemidir.
n>m ve b0 olmak üzere, ifadesinin pay ve paydası ile çarpılarak paydası kökten kurtarılır.
- ifadesinde paydalar sırasıyla ile çarpılır ise ifade halini alır.
- ifadesi yukarıdaki yönteme uygun şekilde çarpılır ise
- olur.
- Paydalar eşitlenir ise,
- bulunur.
Eşlenik Alarak Paydayı Kökten Kurtarma
Çarpanları rasyonel olan iki irrasyonel sayıdan her biri diğerinin eşleniği olarak tanımlanır. Köklü rasyonel ifadelerde, paydayı kökten kurtarmak için paydadaki sayının eşleniği ile pay ve payda çarpılır.
| Sayı | Eşleniği | Sayı . Eşlenik |
|---|---|---|
| , [n=a+b] |
Özel Köklü İfadelerin Hesaplanması
Birinci Durum
olduğundan, paydada veya ifadelerinden biri varken diğeri ile pay ve payda çarpılarak paydada a-b elde edilir.
İkinci Durum
şeklindeki ifadelerde, (a>b) ise,
eşitlikleri göz önünde bulundurulmalıdır.
Başka bir ifadeyle; x=a+b, y=a.b ve a>b olmak üzere; veya olur.
Örnek: işleminin sonucunu bulalım.
Çözüm: dir.
İç İçe Kökler
Örnek: tir.
Köklü Sayılarda Sıralama
Köklü sayılarda sıralama yapılırken kök dereceleri eşitlenir. Daha sonra kök içindeki değerlere göre sıralama yapılır.
dir.
Örneğin ifadeleri sıralanırken kök dereceleri 12 de eşitlenir. Bu durumda a=, b=, c= olur. 56>64>29 olduğundan a>b>c dir.
Oran ve Orantı
Konu Özeti
Aynı türden iki çokluğun bölme yoluyla karşılaştırılmasına oran denir. İki oranın eşitliğine ise orantı denir.
x, y ve z sayıları sırasıyla a, b ve c sayıları ile doğru orantılı ise olur.
Not: a ve b sıfırdan farklı reel sayılar olmak üzere, y= ax + b eşitliğini sağlayan x ve y değerleri doğru orantılı değildir. Ancak, x in değişme miktarı ile y nin değişme miktarı doğru orantılıdır.
Ters Orantı
İki çokluktan biri artarken diğeri de aynı oranda azalıyorsa bu iki çokluk ters orantılıdır denir. Ters orantılı iki çokluğun çarpımı sabittir.
y ile x ters orantılı ise, y.x=k veya olur.
in grafiği aşağıdaki gibidir.

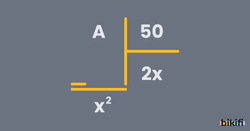

Hiç yorum yok:
Yorum Gönder
Yorumunuza en kısa zamanda okunup cevap atılacaktır